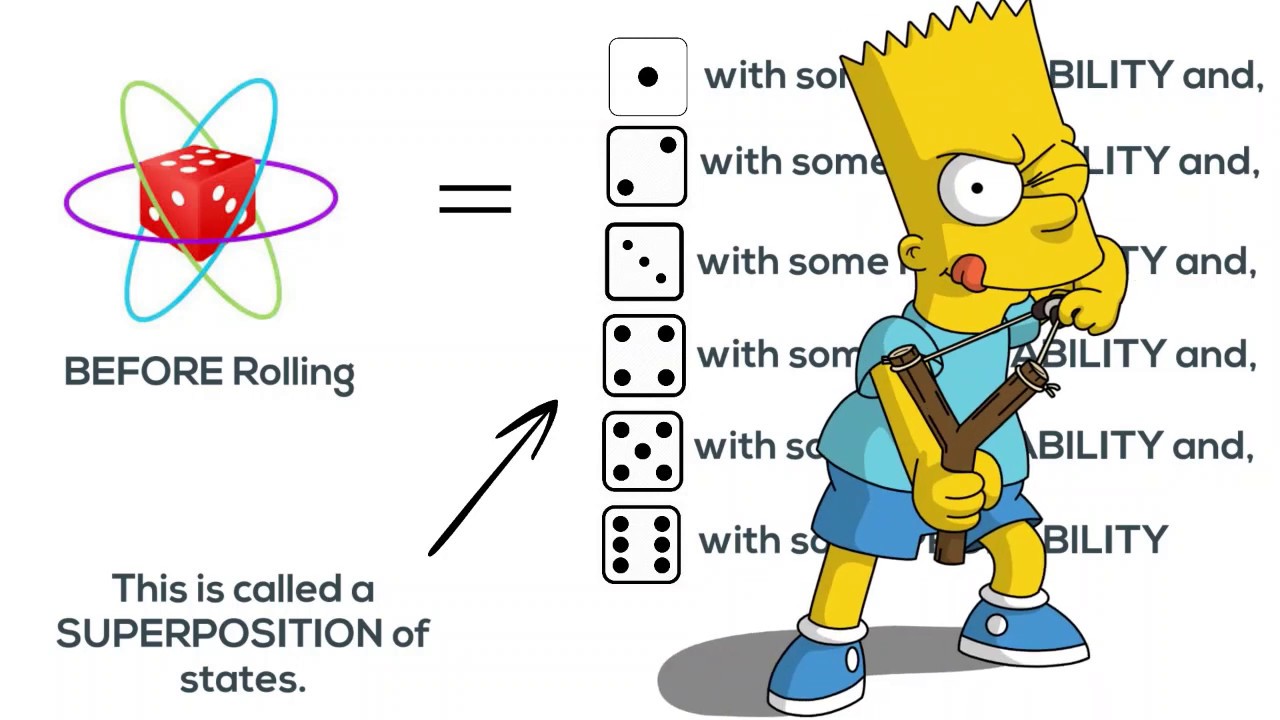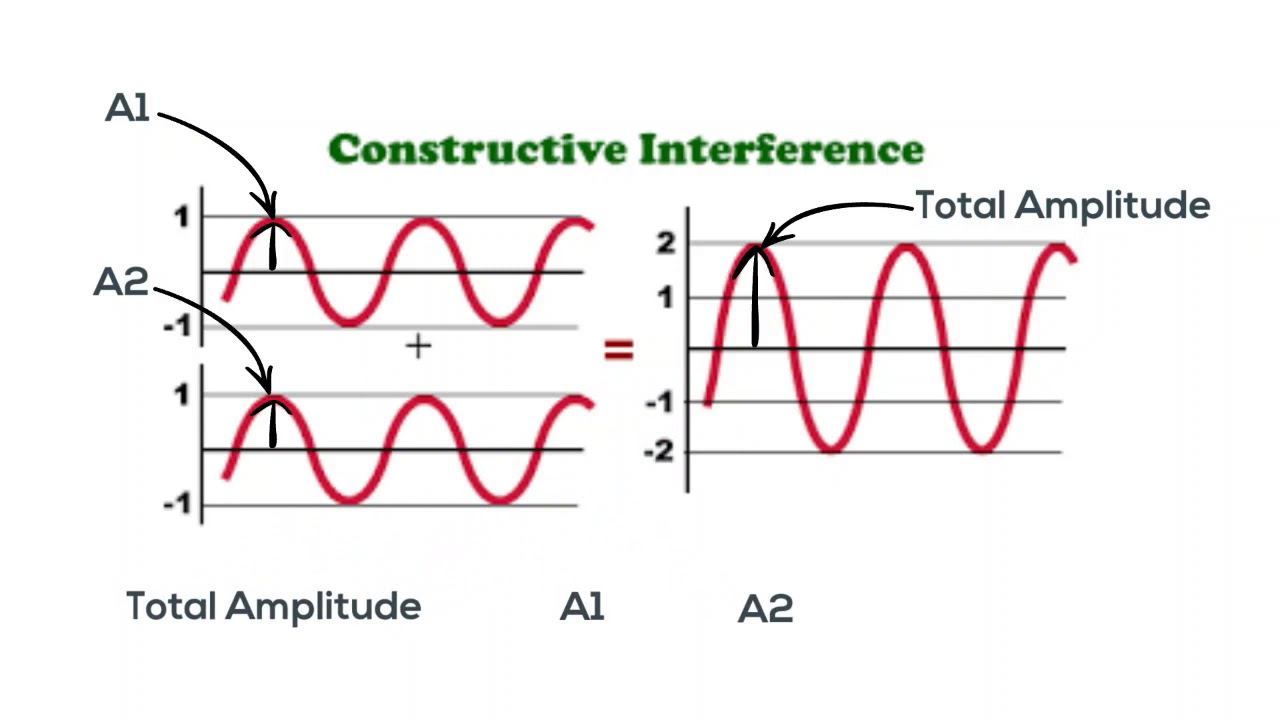
WELCOME TO THE PARTICLE EXPERIENCE
An invitation to the study of everything
Yo.
Who we are: People who like physics.
What we do: Make videos and blog posts about physics.
Hopes and Dreams: That you learn about the Universe, from the very small, to the very big.
Supported in part by the National Science Foundation (NSF) through CAREER grant PHY-1756996.
SNEAK PEEK
Find below a sneak peek of some of the topics we have covered, or hope to cover!
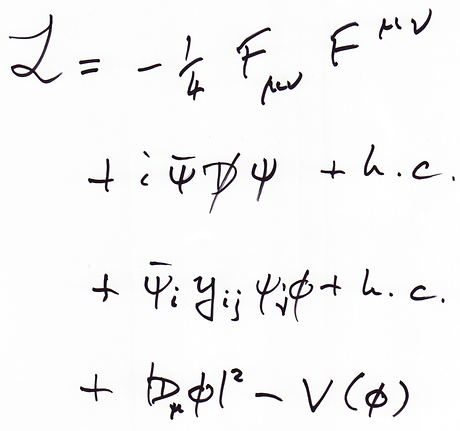
THE STANDARD MODEL
The Standard Model describes (almost all of) the most fundamental particles in nature and (almost all of) their interactions. It is widely regarded as the most accurate and successful theory in all of science. Among the many outstanding predictions of the Standard Model are the fact that particles like Protons and Neutrons are made up of even smaller constituents called Quarks, the need for every fundamental particle to have an associated anti-particle, and the existence of the Higgs Boson -- famously referred to as the "God Particle".
SUPERSYMMETRY AND STRING THEORY
Where the Standard Model falters is in its cold treatment of Einstein's theory of Gravitation. Enter two of the biggest ideas in contemporary Physics which claim to come to the rescue. String Theory presents a drastically changed view of our universe in which the fundamental players are not particles, but tiny vibrating strands of energy called strings. Coupled with supersymmetry (SUSY for short), many believe this could be the heralded "Theory of Everything".


DARK MATTER, DARK ENERGY, AND THE COSMOLOGICAL CONSTANT PROBLEM
According to Einstein's theory of Gravitation the rate of expansion of the universe should be uniformly decreasing in time. However, predictions for the age of the universe using this logic prove drastically inaccurate in the face of astronomical evidence. This has lead Cosmologists to conjecture that the rate of expansion of the universe is accelerating rather than slowing down. Their explanation: there are unseen, undetected gravitational sources spurring on the rate of expansion. Fittingly, we refer to these sources as Dark Matter and Dark Energy, precisely because we cannot see them.